Entwicklung einer Bewegungsbibliothek
Projektarbeit von Hao Wu, Jing Xian und Xiaofeng Tong (10/2009)
Die Aufgabestellung der Projektarbeit lautete, eine Menge von Posen (Servostellungen für sinnvolle Roboterhaltungen) zusammenzustellen, die Nachfolgerelation (aller zulässigen Folgeposen mit einem Kostenparameter für den Zeitaufwand) aufzustellen und Notfallstrategien für Anomalien (auf den Rücken gefallen, auf den Bauch gefallen, unterschiedliche Kollisionssituationen mit Hindernissen etc.) zu entwickeln.
Web-Seiten mit Informationen zur Arbeit
Grundlage der Arbeit
Robonova-I
Ein humanoider Roboter ist ein Roboter, dessen Konstruktion der menschlichen Gestalt nachempfunden ist. Häufig sind die Positionen der Gelenke und die Bewegungsabläufe eines humanoiden Roboters von den menschlichen Gelenkpositionen und Bewegungsabläufen inspiriert. Unter anderem läuft ein humanoider Roboter meistens auf zwei Beinen. Eine dem Menschen in seinem Aussehen und Verhalten besonders ähnliche Form des humanoiden Roboters ist der Robonova-I.
Der Robonova-I von HiTEC ist ein humanoider Roboter für Einsteiger und Fortgeschrittene.
Der Roboter ist sehr beweglich. Er besitzt 16 Gelenke (10 Beingelenke und 6 Armgelenke) und überzeugt durch eine moderne und robuste Ausführung aller Teile.
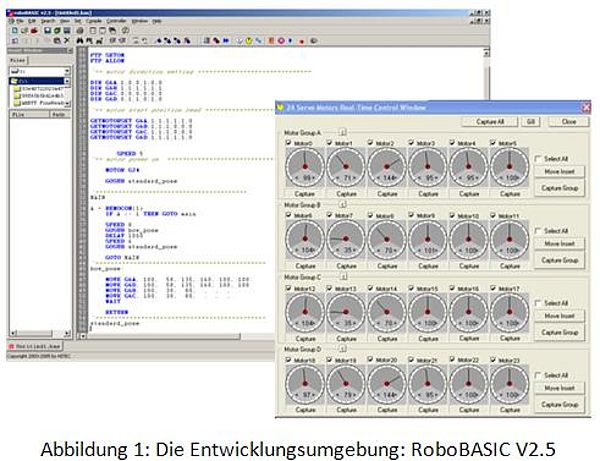
Entwicklungsumgebung
Robonova-I lässt sich grundsätzlich mit drei Programmen programmieren. Mit Hilfe der drei Softwares können auf einem PC mit Windows-Betriebssystem (ab Windows 98) die Bewegungsabläufe des Robonovas entwickelt und seine Reaktionen auf Sensorereignisse festlegt werden:
- ROBOSCRIPT ist ein Skript-Programm für die Robotersteuerung.
- ROBOREMOCON ist einen Roboter zu steuern Programm wie als IR-Fernbedienung.
- ROBOBASIC ist eine BASIC-Compiler für die Robotersteuerung.
ROBOBASIC
RoboBASIC ist ein für die Programmierung des Robonova-I optimierter Basic-Dialekt. RoboBASIC stellt eine Erweiterung der allgemeinen Grundprogrammiersprache mit Befehlen zur Steuerung von Robotern dar.
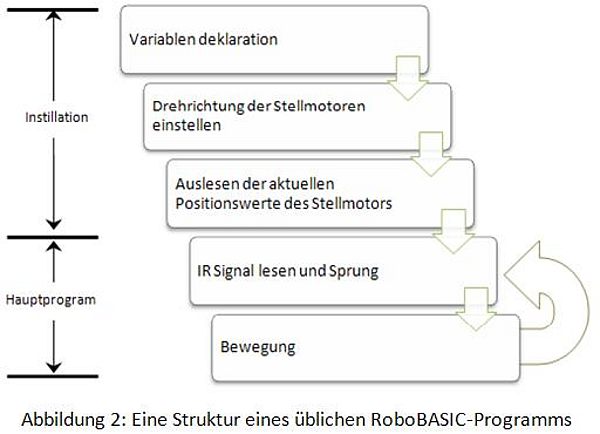
Ein übliches RoboBASIC-Programm hat eine bestimmte Struktur, die verfolgt werden muss, um eine richtige Bewegung von Robonova zu erstellen:
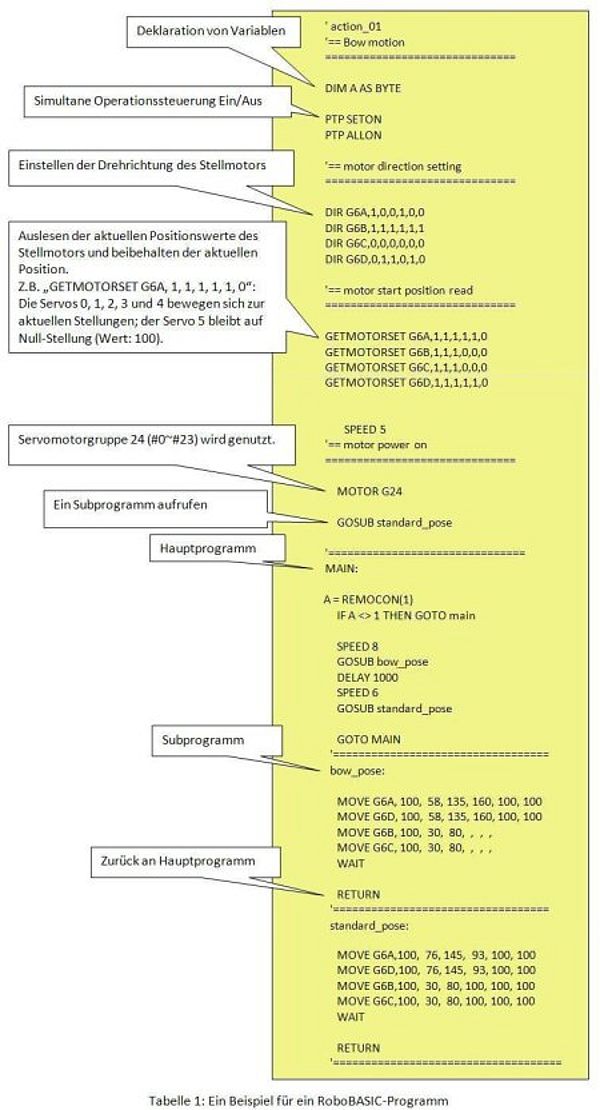
Als Beispiel ist das Programm (Bow motion) unten dargestellt:
Das Control Board
Das Control Board (MR C-3024) ist das "Herz" des Robonova-I. Das Board ist an der Rückseite des Roboters durch eine Abdeckung gesichert. Auf den Board befindet sich ein ATMega128L Prozessor. Er besitzt einen interne 64k*8 EEPROM als Programmspeicher. Zusätzlich befindet sich auf dem Board ein externer Speicher.
Technische Daten MR C-3024:
- Controller: Atmel ATMega128L
- Abmessungen ca.: 61 x 50,5mm
- Betriebsspannungsbereich: 6 -8 Volt
- I/O Ports:
- 40 Ports auf Pfostensteckern, davon 24 als Servoports und 8 als A/D Wandler
- 2*RS232 Schnittstellen
- Signalgeber
- Zusatz Speicher: 64K *8 EEPROM
Grundbewegungen
In einem Demoprogramm sind 28 Beispielabläufe für Grundbewegungen programmiert (Tabelle 2). Jeder Grundbewegung ist eine Tastennummer zugeordnet, mit der sie aktiviert wird.
GBNr. | Name der Grundbewegung | GBNr. | Name der Grundbewegung |
1 | Bow (Verbeugung zur Begrüßung) | 2 | Hands Up (Hände über den Kopf) |
3 | Sit Down (Setzen) | 4 | Sit Down and Raise Hands (Setzen, und Hände über den Kopf) |
5 | Raise Left Leg (Link Bein heben) | 6 | Simple Dance (Ein einfacher Tanz, der Körper schwingt links und rechts) |
7 | Flying * (Hände  bewegen, wie der Bogel-Flug) | 8 | Left and Right Kick (Links und rechts schießen) |
9 | Headstand (Stand suf dem Kopf) | 10 | Fast Walk (Schnell laufen) |
11 | Turn Left * (Links drehen) | 12 | Turn Right * (Rechts drehen) |
13 | Forward Walk * (Vorwärts laufen) | 14 | One Step Left * (Schritt nach links) |
15 | Sit Down and Stand Up (Setzen und aufstehen) | 16 | One Step Right * (Schritt nach rechts) |
17 | Backward Walk * (Rückwärts laufen) | 18 | Forward Tumbling (Rad schlagen vorwärts) |
19 | Left Tumbling (Rad schlagen links) | 20 | Punch (Angriff) |
21 | Right Tumbling (Rad schlagen rechts) | 22 | Backward Tumbling (Rad schlagen rückwärts) |
23 | Left Hand Attack (Links Angriff) | 24 | Right Hand Attack (Rechts Angriff) |
25 | Sit Down and Left Punch (Setzen und links Angriff) | 26 | Sit Down and Right Punch (Setzen und rechts Angriff) |
30 | Forward Get Up (Aufstehen <Bauch>) | 31 | Backward Get Up (Aufstehen <Rücken>) |
GBNr. - Grundbewegungsnummer;
*Â Â Â Â- Grundbewegungen, die meist mehrfach nacheinander auszuführen sind.
Tabelle 2: Grundbewegungen für RoboBASIC (bas)
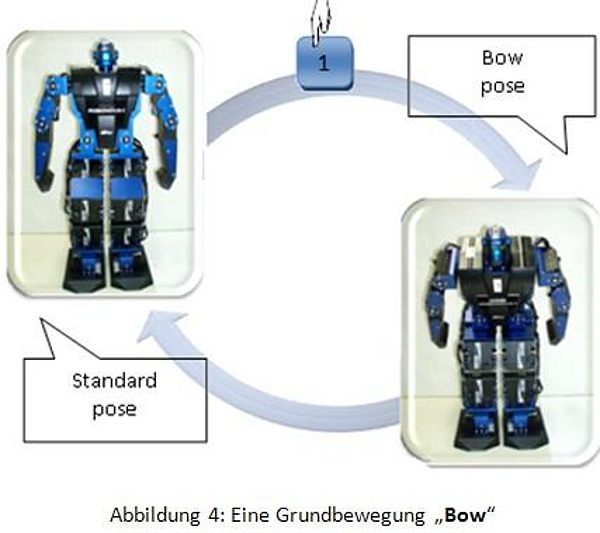
Die Abbildung 4 zeigt ein Beispiel für die Grundbewegungen: "Bow".
XML-Dokument
Die Extensible Markup Language (engl. für "rweiterbare Auszeichnungssprache", abgekürzt XML, ist eine Auszeichnungssprache zur Darstellung hierarchisch strukturierter Daten in Form von Textdaten. XML wird u.a. für den Austausch von Daten zwischen Computersystemen eingesetzt, speziell über das Internet.
A. Aufbau eines XML-Dokuments:
Ein jedes XML-Dokument besteht dabei aus dem Prolog, dem Wurzelelement (und seinen Inhalten) sowie Verschiedenem.
1. Der Prolog: Der Prolog besteht zunächst aus der XML-Deklaration:
<?xml version="1.0" encoding="utf-8"?> |
welche die Version des XML-Dokumentes sowie den Zeichensatz angibt, in dem das Dokument verfasst wurde. Optional folgen die Dokumententypdefinition (DTD) sowie Verarbeitungsanweisungen und Kommentare.
<?xml version="1.0" encoding="utf-8"?> <!DOCTYPEÂ WurzelElement SYSTEM "index.dtd"> <!-- ein Beispiel von XML-Dokument. --> |
2. Wurzelelemente:Â Ein XML-Dokument hat ein Wurzelelement, welches alle anderen Elemente und deren Inhalte umschließt.
<WurzelElement>    <Inhalt>Erstes XML-Dokument</Inhalt>    <Text> Das erste Beispiel für ein           wohlgeformtes XML-Dokument    </Text> </WurzelElement> |
3. Verschiedenes: Nachdem ein Wurzelelement geschlossen ist, sind nur noch Kommentare erlaubt.
<!-- Ende des XML-Dokumentes --> |
B. Beispiel eines XML-Dokumentes:
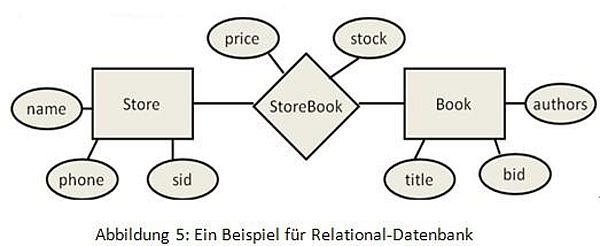
Umwandlung relationale Datenbanken in XML :
Relational Datenbank:
      Store (sid, name, phone)
      Book (bid, title, authors)
      StoreBook (sid, bid, price, stock)
Das entsprechende XML:
        <store> <name> ... </name>
                      <phone> ... </phone>
                      <book>  <title>...        </title>
                                 <authors> ... </authors>
                                 <price> ...       </price>
                      </book>
                      <book>...</book>
                      ...
        </store>Endlicher Automat
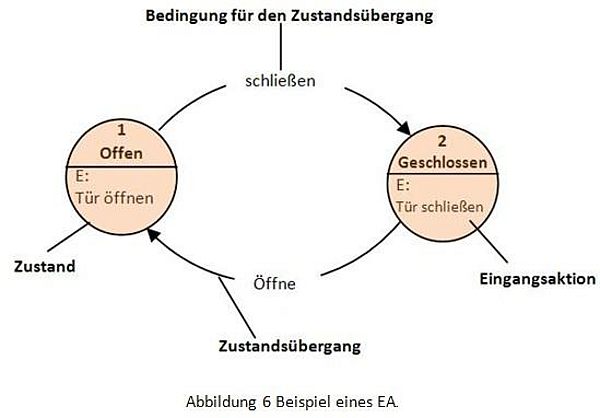
Ein endlicher Automat (EA, auch Zustandsmaschine, englisch finite state machine (FSM)) ist ein Modell des Verhaltens, bestehend aus Zuständen, Zustandsübergängen und Aktionen.
Ein Automat heißt endlich, wenn die Menge der Zustände, die er annehmen kann (später S genannt), endlich ist. Ein EA ist ein Spezialfall aus der Menge der Automaten. Ein Zustand speichert die Information über die Vergangenheit, d.h. er reflektiert die Änderungen der Eingabe seit dem Systemstart bis zum aktuellen Zeitpunkt.
Ein Zustandsübergang zeigt eine Änderung des Zustandes des EA und wird durch logische Bedingungen beschrieben, die erfüllt sein müssen, um den Übergang zu ermöglichen. Eine Aktion ist die Ausgabe des EA, die in einer bestimmten Situation erfolgt.
Es gibt vier Typen von Aktionen:
- Eingangsaktion : Ausgabe wird beim Eintreten in einen Zustand generiert.
- Ausgangsaktion : Ausgabe wird beim Verlassen eines Zustandes generiert.
- Eingabeaktion : Ausgabe wird abhängig vom aktuellen Zustand und Eingabe generiert.
- Übergangsaktion: Ausgabe wird abhängig von einem Zustandsübergang generiert.
Ein EA kann als Zustandsübergangsdiagramm wie in Abbildung 6 dargestellt werden. Zusätzlich werden mehrere Typen von Übergangstabellen (bzw. Zustandsübergangs- tabellen) benutzt. Die folgende Tabelle zeigt eine sehr verbreitete Form von Übergangstabellen: die Kombination aus dem aktuellen Zustand (B) und Eingabe (Y) führt zum nächsten Zustand (C). Die komplette Information über die möglichen Aktionen wird mit Hilfe von Fußnoten angegeben. Eine Definition des EA, die auch die volle Ausgabeinformation beinhaltet, ist mit Zustandstabellen möglich, die für jeden Zustand einzeln definiert werden.
Übergangstabelle | |||
Momentaner Zustand/Bedingung | Zustand A | Zustand B | Zustand C |
Bedingung X | ... | ... | ... |
Bedingung Y | ... | Zustand C | ... |
Bedingung Z | ... | ... | ... |
Tabelle 3. Übergangstabelle eines EAs
Zustandsmaschinen werden hauptsächlich in der Entwicklung digitaler Schaltungen, Modellierung des Applikationsverhaltens (Steuerungen), generell in der Softwaretechnik sowie Wort- und Spracherkennung benutzt.
Phasenstruktur von Bewegungen
Im Allgemeinen wird zwischen zyklischen und azyklischen Bewegungen unterschieden.
Azyklischen Bewegungen
Bei azyklischen Bewegungen wird das Bewegungsziel durch eine einmalige Aktion erreicht (Beispiel: Werfen, Springen). Die Reihenfolge der Teilbewegungen ist nicht umkehrbar. Die Bewegung kann dabei in drei Phasen gegliedert werden:
- Es lässt sich Vorbereitungs-, Haupt-, und Endphase unterscheiden.
- Jede Teilbewegung hat eine besondere Funktion im Gesamtablauf.
- In der Hauptphase wird das eigentliche Bewegungsziel erreicht.
- Vorbereitungsphase (Auftakt)
Zunächst müssen günstige Voraussetzungen für das Lösen der Bewegungsaufgabe geschaffen werden.
- Hauptphase (Akzent)
In der Hauptphase wird die eigentliche Bewegungsaufgabe gelöst.
- Endphase (Abfangen/Abtakt)
Zum Abschluss muss der Körper wieder in eine Gleichgewichtsposition gebracht bzw. abgebremst werden.
Zyklischen Bewegungen
Bei zyklischen Bewegungen wiederholen sich gleichartige Teilbewegungen (Beispiel: Laufen). Der Bewegungsablauf lässt sich in zwei Phasen einteilen. Es kommt zu einer Überlagerung von Vorbereitungs- und Endphase (Phasenverschmelzung).
- Die Struktur der Bewegung wird dann als Haupt- und Zwischenphase bezeichnet.
- Bei einer Reihe von Bewegungen kommt es zu einer Kombination von zyklischen und azyklischen Bewegungen.
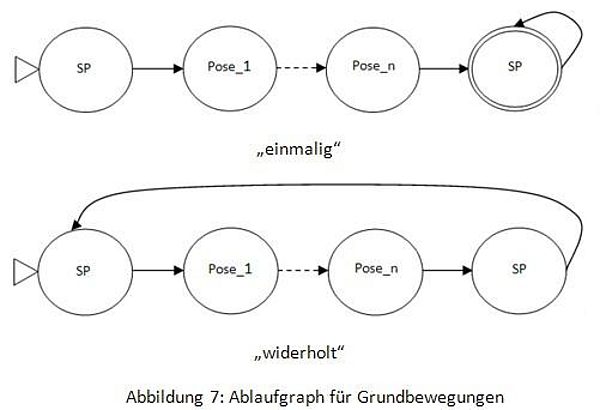
Die Grundbewegungen lassen sich einteilen in azyklische Abläufe, die meist nur einmal nacheinander ausgeführt werden (schießen, Handstand etc.) und zyklische Abläufe, die meist mehrfach nacheinander ausgeführt werden (Schritt nach vorn).
Mit RoboBASIC können zwei programmierte Bewegungen entweder fest verkettet werden oder zwischen zwei Bewegungen wird auf eine Eingabe über die Fernbedienung gewartet. Eine feste Verkettung hat den Nachteil, dass nur genau die programmierte Bewegung, z.B. drei Schritte nach vorn, ausgeführt wird, ohne dass sie unterbrochen oder verändert werden kann.
Jede Abfrage kostet Zeit, während dieser der Bewegungsfluss unterbrochen ist. Ziel der Arbeit ist es, dass variable Bewegungen gesteuert werden können, ohne dass der Bewegungsfluss durch das Warten auf Eingaben unterbrochen wird.
Definitionen und Begriffsbestimmungen
Pose
Jede Bewegung lässt sich in verschiedene Bewegungsabschnitte einteilen, die jeweils für das Gelingen der Bewegung eine unverzichtbare Funktion haben.
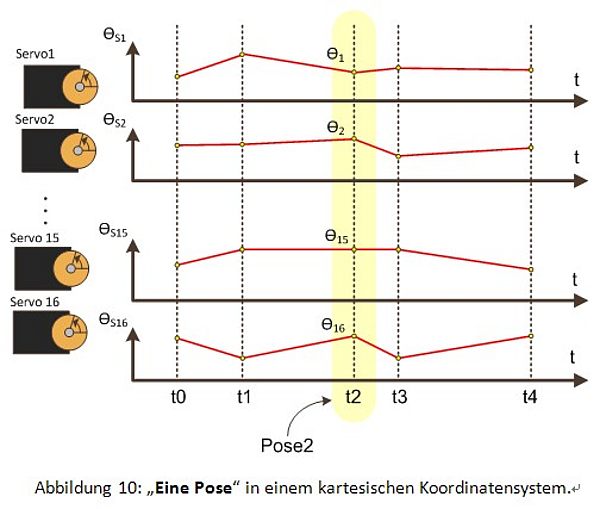
Als Pose wird in technischem Kontext die Kombination von Position und Orientierung eines Objekts bezeichnet.
Nach DIN EN ISO 8373 (Industrieroboter Wörterbuch) ist die Pose die Kombination von Position und Orientierung im dreidimensionalen Raum. Die Position einer punktförmigen Masse in Relation zu einem kartesischen Koordinatensystem definiert sich demnach durch die Abstände entlang den Koordinatenrichtungen x, y, z. Wird an diesem Massepunkt ein zweites kartesisches Koordinatensystem aufgespannt, so definiert sich die Orientierung dieses Koordinatenkreuzes durch den Winkelversatz seiner Koordinatenachsen in Bezug zu den entsprechenden Achsen des Basiskoordinatensystems. Es sind somit zusätzlich drei Winkel notwendig, die die Lage des neuen Koordinatensystems bezogen auf das Basiskoordinatensystem beschreiben.
In dieser Arbeit ist die Pose eine von verschiedenen Servostellungen für sinnvolle Roboterhaltungen. Das heißt, jede Pose hat ihre eigenen Parameter, die aus Positionen aller Gelenke zu einem bestimmten Zeitpunkt bestehen. Solche Parameter sollten gleichzeitig an die Gelenke geschickt werden.
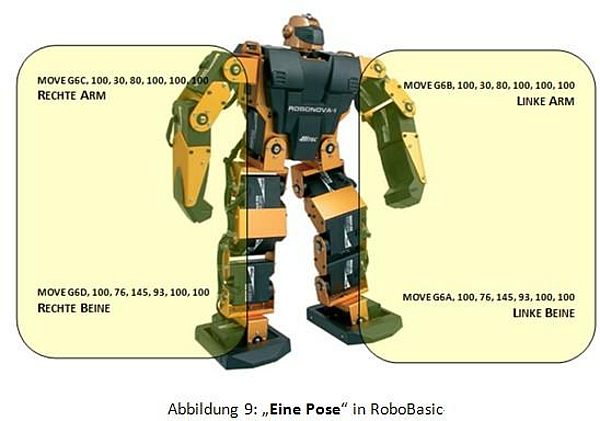
Die Abbildung 9 zeigt ein Beispiel einer Pose, wobei die Nummern die Parameter darstellen.
- "MOVE"steuert mehrere Servos gleichzeitig.
- "G6A" ist die Gelenkgruppe mit den Servos 0 bis 5.
- "G6B"die für die Servos 6 bis 11.
- "G6C"die für die Servos 12 bis 17.
- "G6D"die für die Servos 18 bis 23.
Die Werte definieren die Winkelstellungen der entsprechenden Gelenke.
Beim Laufen bewegt der Roboter mindestens ein Gelenk.
Zu einem bestimmten Zeitpunkt hat jedes Gelenk eine bestimmte Winkelstellung. Eine Pose des Roboters kann als ein Tupel der Winkelstellungen aller Gelenke beschrieben werden. Z.B. kann man eine Pose wie Folgende beschreiben:
Z-Pose
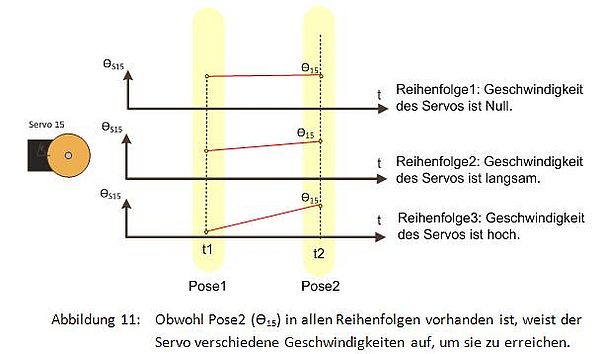
Um eine Pose zu erreichen, braucht der Roboter Zeit. Diese Zeit ist von vielen Faktoren abhängig, z.B. vom Unterschied zwischen dem momentanen θ-Vektor und dem letzten θ-Vektor, d.h. die Pose hat in einer bestimmten Reihenfolge von Posen besondere Eigenschaften. Wenn sie sich in einer anderen Reihenfolge von Posen befindet, muss sie anders behandelt werden. Dies wird als Z-Pose bezeichnet.
Z-Pose ist eine Pose mit zusätzlichen Beschreibungselementen für den zeitlichen Bewegungsablauf. Die Beschreibungselemente für den zeitlichen Bewegungsablauf sind:
- speed <Wert>;
- highspeed seton/setoff;
- wait;
- delay <Wartezeitt>.
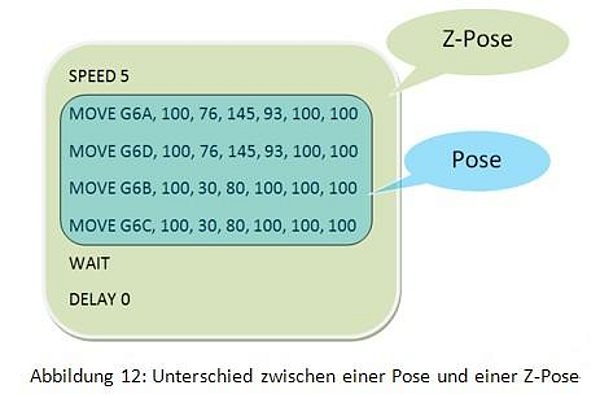
Die Abbildung 12 zeigt den Unterschied zwischen einer Pose und einer Z-Pose in RoboBasic.
- Mit dem Befehl "SPEED" wird die Geschwindigkeit aller Servomotors eingestellt. Der Einstellbereich liegt zwischen 1 (sehr langsam) und 15 (sehr schnell).
- Die Funktion von "WAIT", ist zu warten, bis die Z-Pose vollständig ausgeführt ist. Damit sich alle Servos synchron bewegen, müssen zuerst die neuen Werte an alle Motorgruppen zugewiesen werden. Der Controller stellt dabei die Drehgeschwindigkeit aller Servos so ein, dass die Bewegungen zur gleichen Zeit enden.
- "DELAY" heißt, dass die Programmausführung für eine festgelegte Zeit unterbrochen wird.
In dieser Arbeit hat jede Z-Pose einen eigenen Kurznamen, z.B. B_p1 für Bow_Z-Pose_1 und B_sp für Bow_Z-Standard_ Pose.
Bewegung
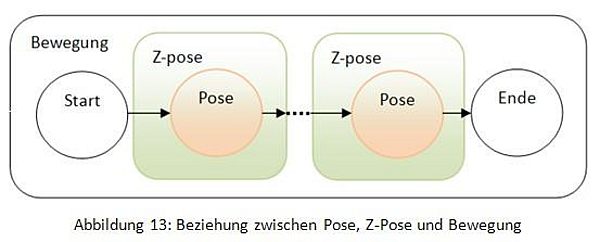
Eine Bewegung wird durch die Abarbeitung einer Folge von Z-Posen beschrieben.
In den BNF (Backus-Nauer-Form) besteht eine Bewegung aus mindestens zwei Z-Posen, den beliebig viel weitere Z-Posen folgen dürfen:
<Z-Pose> {<Z-Pose>}
(<Z-Pose> -- Teilprogramm zur Steuerung einer Z-Pose; {} - Notation für beliebig oft).
Bewegung = ∑(Z-Pose)
Die Abbildung 13 zeigt die Beziehung zwischen Pose, Z-Pose und Bewegung:
Bewegungsfluss
Die flüssige Bewegung ist:
- runde, nicht eckige Bewegungen.
- allmählich, nicht plötzlich, nicht abrupt.
- fließende Übergänge im Kraftverlauf.
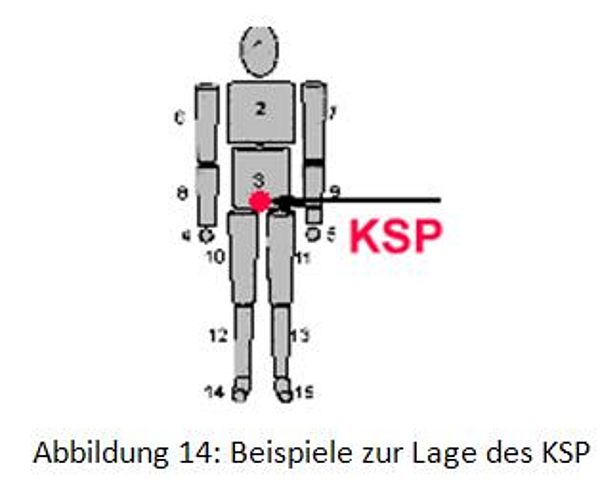
Körperschwerpunkt
Der Körperschwerpunkt (KSP) ist ein fiktiver Punkt, in dem die Masse des gesamten Körpers und Angriffspunkt der Schwerkraft gedacht werden kann.
Anders formuliert:
Im KSP halten sich die Schwerkraftmomente aller Masseteile die Waage. Besondere Bedeutung hat der KSP deshalb, weil er als Angriffspunkt für die Schwerkraft bei jeder Bewegung wichtig ist (Angriffs-punkt aller äußeren Kräfte).
Im Gegensatz zu starren Körpern gibt es jedoch beim Menschen bzw. Robotern keinen festen KSP. Er ist abhängig von der Körperposition und der Masseverteilung im Körper.
Mehre Folgeposen
Eine Folgepose ist ein möglicher Nachfolger einer Z-Pose. Möglich bedeutet, dass die nachfolgende Z-Pose sich so an den Vorgänger anschließt, dass eine sinnvolle Bewegung herauskommt, z.B. das der Roboter läuft, ohne umzufallen. Manche Z-Posen haben nur einen Nachfolger, manche haben mehrere oder wie die Grundstellung (aufrecht stehen) viele Nachfolger.
In einer Grundbewegung hat jede Z-Pose genau einen Nachfolger. Der Roboter arbeitet immer genau eine Grundbewegung ab. Diese wird durch eine Variable mit der Nummer der Grundbewegung festgelegt.
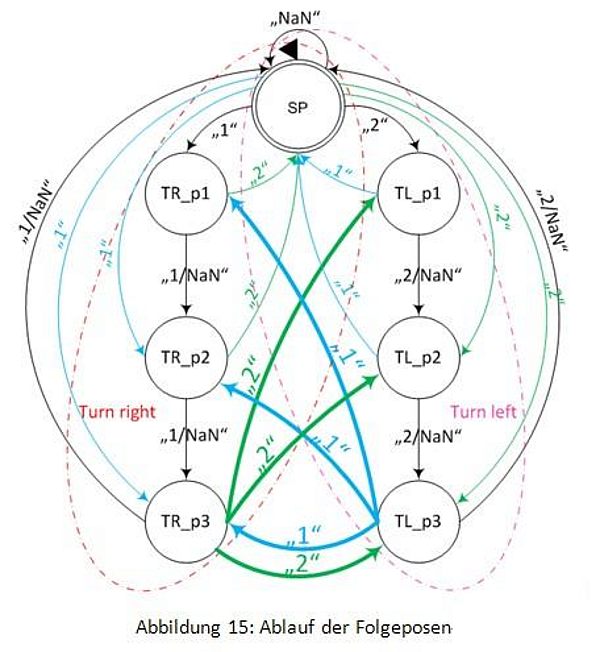
In der Abbildung 15 wird die Folgepose mit Hilfe eines Beispiels mit zwei Bewegungen erklärt. Der Verlauf der schwarzen Linien stellt die originalen Bewegungen "Turn_right" (links) und "Turn_left" (rechts) dar.
Nach jeder originalen Z-Pose einer Grundbewegung "Turn_right" können drei Nachfolger aus der Grundbewegung "Turn_left" eingesetzt werden. Diese drei Nachfolger sind "TL_p1→TL_p2→TL_p3→SP", "TL_p2→TL_p3→SP" und "TL_p3→SP". Sie werden "TL_z1", "TL_z2" und "TL_z3" genannt. Aber nicht alle Nachfolger können Folgeposen sein. Z.B. hat "TR_p1" nur eine Folgepose (der Verlauf der dünnen grünen Linie); aber "TR_p3" hat drei Folgepose (der Verlauf der dicken grünen Linien).
Nach jeder originalen Z-Pose einer Grundbewegung "Turn_left" können auch drei Nachfolge aus der Grundbewegung "Turn_right" eingesetzt werden. Diese drei Nachfolger sind "TR_p1→TR_p2→TR_p3→SP", "TR_p2→TR_p3→SP" und "TR_p3→SP". Sie werden "TR_z1", "TR_z2" und "TR_z3" genannt. Die Situation ist die gleiche wie die oben beschriebene. Die Abläufe werden mit blauen Linien gezeigt.
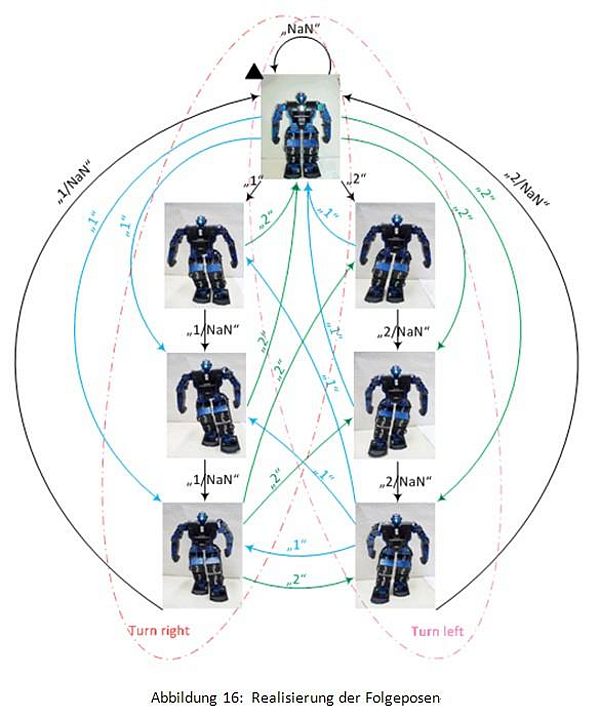
Im Vergleich zur Abbildung 15 kann dieses Beipiel der Folgepose mit Hilfe der Abbildung 16 besser verstanden werden.
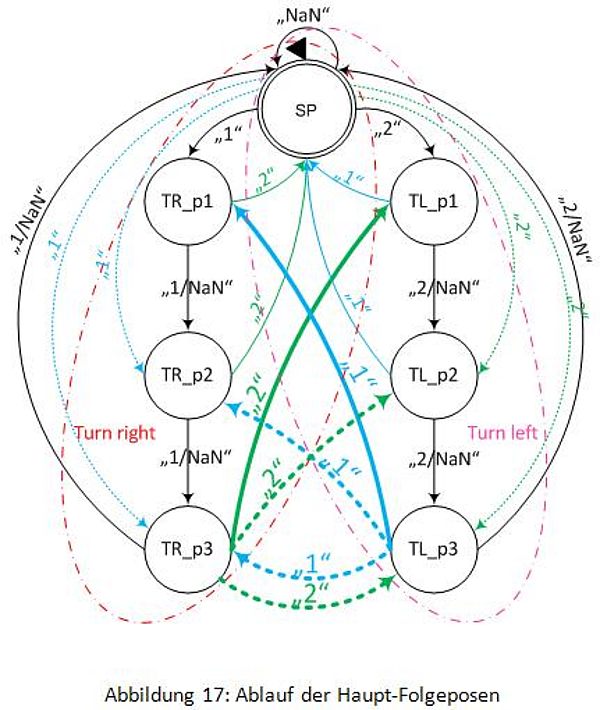
Die Haupt-Folgeposen
"Haupt" bedeutet hier "am Besten". Das heißt, dass die Haupt-Folgeposen die besten Folgeposen aus allen Folgeposen sind, damit der Roboter sich flüssig und stabil bewegen kann.
- Eine flüssige Bewegung muss rund, allmählich, nicht plötzlich sein und zeigt aber auch fließende Übergänge im Kraftverlauf.
- Eine stabile Bewegung zeigt sich bei mehreren Abläufen, die einigermaßen das gleiche Ergebnis aufweisen, auch wenn die Abläufe auf unterschiedlichem Untergrund gemacht werden. Die Schwingungen des Roboters treten bei einer stabilen Bewegung im zulässigen Bereich ein, wobei die unzulässigen Schwingungen zum Umfallen des Roboters führen.
Die Abbildung 17 zeigt den Ablauf der Haupt-Folgeposen (der Verlauf der dicken Linien). Die Verläufe der gestrichelten Linien bedeuten, dass der Roboter sich nicht mehr flüssig oder/und nicht mehr stabil bewegen kann.
Arbeitsfolge
Konkret verfolgt diese Arbeit die wesentlichen Schritte:
Zusammenstellen einer Menge von Z-Posen
Die orginalen Bewegungsporgramme waren nur als fließendes Skript geschrieben. Mit solchen Skripten und im Laufe des Entwicklungsprozesses der Programmierung ergibt sich eine Vielzahl von Schwierigkeiten. So wächst z.B. die Unklarheit des Codes und dieser wird auch immer mehr spezialisiert. Damit ist die Arbeit zum Ende mit der Hand oft fehleranfälliger.
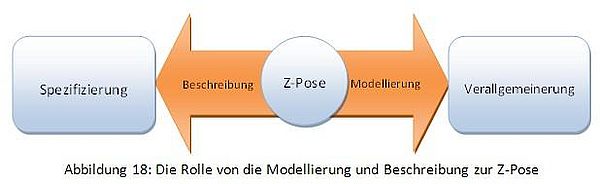
In der Struktur der orginalen Bewegungsporgramme fehlt die Modellierung. Ein Modell ist ein durch Abstraktion (Reduzierung und Verallgemeinerung) gewonnenes Abbild eines bestimmten Ausschnitts der Realität. Die Modellierung ermöglicht viele Szenarien, z.B. können beliebig oft beliebige Szenarien simuliert werden. Außerdem können in der Simulation Dinge beobachtet werden, die im Versuch nicht zugänglich sind. Änderungen können schnell eingeführt und "ausprobiert" werden. Die modellierten Programme sind eine Konstruktion effizienter Programme.
Andererseits müssen Modelle erst aufwändig erstellt werden. Deswegen werden am Anfang dieser Arbeit alle Bewegungen genau untersucht. Daraus entstehen die Eigenschaften und Parameter des Modells der Z-Posen. Danach werden alle Posenserien in verschiedene Z-Posen zerlegt und anschließend alle Z-Posen benannt und beschrieben.
Die Beschreibung der Posen enthält die folgenden Definitionen:
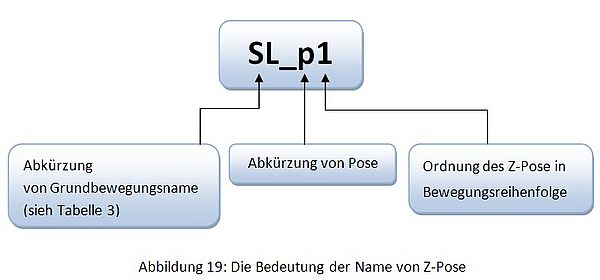
- Name: Der Name der Z-Pose ist eine Abkürzung, in der sich einige Informationen und Eigenschaften der Z-Pose selbst verstecken, zum Beispiel:
- Parameter: Hier stehen die Befehle von RoboBASIC, die durch ihre Ausführung die Z-Pose entstehen lassen.
- Foto: In den Fotos werden bestimmte Posen gezeigt. Dadurch sind solche Posen anschaulicher.
- Beschreibung: Hier dient die Beschreibung der Erkärungen der bestimmten Posen.
- Folge: Hier ist die Folge eine Z-Pose, die in der Grundbewegung der aktuellen Z-Pose folgt.
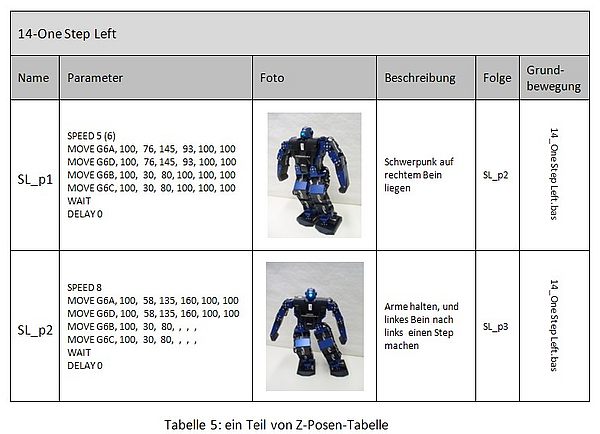
- Grundbewegung: Für die Grundbewegungen sind 28 Beispielabläufe im Demo-programm vorhanden. Hier ist die Grundbewegung zu finden, zu der die aktuelle Z-Pose gehört.
In der Tabelle 5 wird ein Teil der Z-Posen-Tabelle gezeigt.
Doku:
Aufstellung der Nachfolgerelation
Um die Nachfolgerelation zu untersuchen, sollten alle Nachfolger nach jeder Z-Pose eingesetzt werden. Dann werden alle Folgeposen und auch alle Haupt-Folgeposen gefunden. Damit müssen zwei Bedingungen beachtet werden, die Stabilität des Roboters und die Flüssigkeit der Bewegung.
Die Stabilität des Roboters bedeutet, dass der Roboter sich im stabilen Zustand befindet. D.h., der Roboter muss sich stabil bewegen, nicht pendelnd.
Die Flüssigkeit bedeutet, dass der Roboter sich harmonisch bewegen muss und es keine sprunghafte Bewegung gibt.
In diesem Schritt sollen solche Nachfolgerelationen untersucht werden, welche stabilen Z-Posen in Grundbewegungen eingefügt werden können, um die neue Bewegung zu realisieren. Ein Teil der Nachfolgerelation-Tabelle (Bewegung "Bow" nach Bewegung "Sit_down") wird in der Tabelle 6 gezeigt.
Die Beschreibung der Nachfolgerelation enthält die folgenden Definitionen:
Bewegung: Sieh hier
Folge: Folge ist die nächste Z-Pose der vorhandene Z-Pose in einer Grundbewegung.
Mehre Folgeposen: Sieh hier
Haupt-Folgeposen: Sieh hier
1_Bow:
| Bewegung | Folge | Mehre Folgeposen | Haupt-Folgeposen | |
| 3_Sit down | SD_p1 | SD_sp | B_z1, B_z2 | B_z1 |
| SD_sp | SD_p1 | B_z1, B_z2 | B_z1 | |
Tabelle 6. Ein Teil von Folgeposen-Tabelle
Diese Nachfolgerelation-Tabelle kann auch in einen endlichen Automat übersetzt werden.
Generell werden grundsätzlich zwei Gruppen von EA unterschieden: Moore- und Mealy-Automaten
- Moore-Automat: Im Moore-Modell werden nur Eingangsaktionen benutzt, d. h., die Ausgabe (Γ) hängt nur vom Zustand (S) ab (S → Γ).
- Mealy-Automat: Im Mealy-Modell werden Eingabeaktionen benutzt, d. h., die Ausgabe (Γ) hängt von Zustand (S) und Eingabe (∑) ab (S Ã ∑ → Γ). Der Einsatz von Mealy-Automaten führt oft zu einer Verringerung der Anzahl zu berücksichtigender Zustände. Die Funktion des EA ist dadurch komplexer und oft schwieriger zu verstehen.
Moore- und Mealy-Automaten sind gleichwertig. Der eine kann in den jeweils anderen überführt werden.
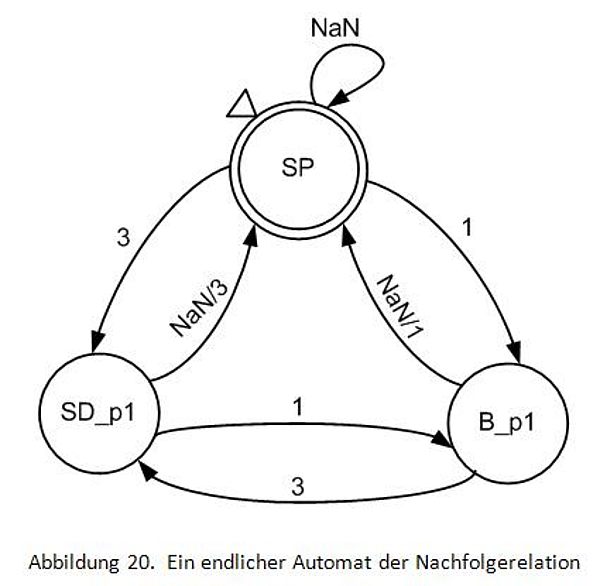
Wegen der möglichen Komplexität des Mealy-Modells ist für die Nachfolgerelation-Tabelle ein Moore-Automat verwendet worden.
Die Abbildung 20 zeigt ein Beispiel von einem endlichen Automaten zwischen Bewegung "Bow" und Bewegung "Sit_down".
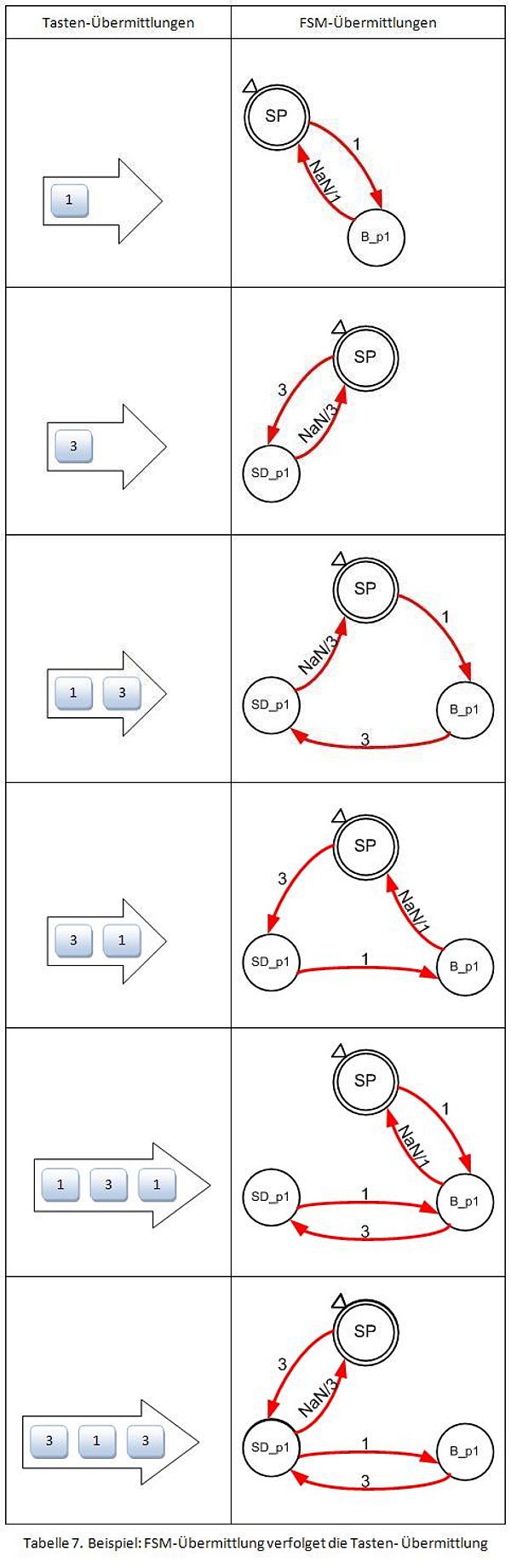
Die Tabelle 7 zeigt, wie die FSM-Übermittlungen (Übertragungen) über die Reihenfolge der gedrückten Tasten verfolgen werden.
Dateien
Herstellung von der XML-Datei
Um die Tabellen in Bibliotheken zu verwenden, werden alle Tabellen als XML-Dateien geschrieben. Die XML-Dateien können als Bibliotheken von vielen Programmiersprachen benutzt werden.
Eine XML-Datei besteht aus verschiedenen Elementen, deren Namen selbst gewählt werden können und die Text beinhalten. Ein Element kann auch Attribute haben. Aus mehreren Elementen ergibt sich dann eine Struktur, die sich der Autor bereits vorher überlegen sollte. Diese Struktur beginnt mit dem Root-Element, das Ausgangspunkt für alle anderen Elemente ist und sie beinhaltet. Die Elemente und die Attribute müssen als ein Paar erscheinen.
In der Tabelle 8 wird ein Teil der XML-Datei für die Z-Posen-Tabelle ("one_step_left") gezeigt. Die Element- und Attribut-Namen in der XML-Datei haben folgende Bedeutungen:
- NewDataSet: das einzig zulässige Wurzelement
- PARTS: die Kindelemente von <NewDataSet>
- Bewegung: der Name der Grundbewegung
- PART: die Kindelemente von <PARTS>
- Pose: der Name der Z-Pose
- High_speed: Der Status der Hochgeschwindigkeitsmodus
- Speed: der Parameter der Geschwindigkeit
- Left_leg: die Winkelstellungen der Gelenkgruppe mit den Servos 0 bis 5
- Right_leg: die Winkelstellungen der Gelenkgruppe mit den Servos 18 bis 23
- Left_hand: die Winkelstellungen der Gelenkgruppe mit den Servos 6 bis 11
- Right_hand: die Winkelstellungen der Gelenkgruppe mit den Servos 12 bis 17
- WAIT: warten, bis das Programm vollständig ausgeführt wurde
- DELAY: Programmausführung um einen gewählten Zeitraum verzögern
<?xml version="1.0" standalone="yes" ?> -<NewDataSet> -<PARTS> <Bewegung>One step left</Bewegung> -<PART> <Z_Pose>SL_p1:</Z_Pose> <High_speed>HIGHSPEED SETOFF</High_speed> <speed>speed 5</speed> <G6A>MOVE G6A, 85, 71, 152, 91, 112, 60,</G6A> <G6D>MOVE G6D, 112, 76, 145, 93, 92, 60,</G6D> <G6B>MOVE G6B, 100, 40, 80, , , ,</G6B> <G6C>MOVE G6C, 100, 40, 80, , , ,</G6C> <WAIT>WAIT</WAIT> <DELAY>DELAY 0</DELAY> </PART> -<PART> <Z_Pose>SL_p2:</Z_Pose> <High_speed>HIGHSPEED SETOFF</High_speed> <speed>speed 9</speed> <G6A>MOVE G6A, 76, 72, 160, 82, 128, 70,</G6A> <G6D>MOVE G6D, 110, 92, 124, 97, 93, 70,</G6D> <G6B>MOVE G6B, 100, 35, 90, , , ,</G6B> <G6C>MOVE G6C, 100, 35, 90, , , ,</G6C> <WAIT>WAIT</WAIT> <DELAY>DELAY 0</DELAY> </PART> ... -<PART> ... </PART> Â </PARTS> ... </NewDataSet> |
        Tabelle 8: ein Teil von XML-Z-Posen-Tabelle "one_step_left"
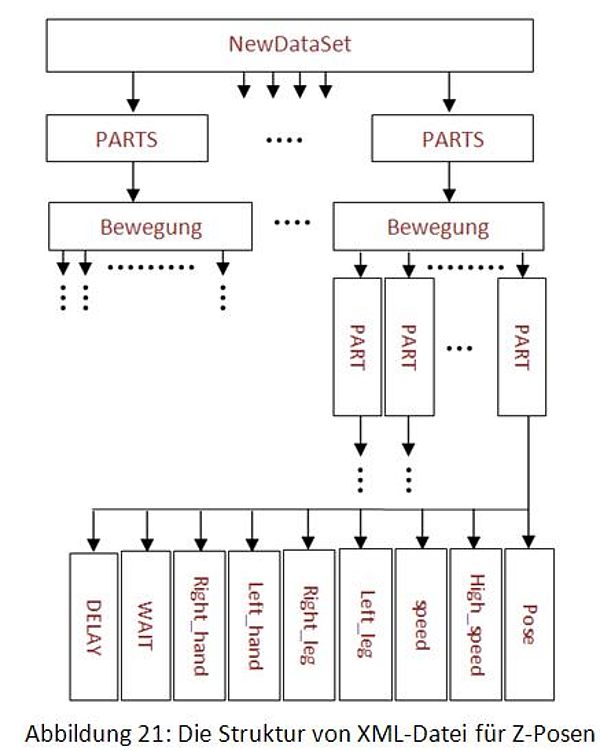
Um die XML-Struktur noch deutlicher zu machen, kann sie als Grafik gezeichnet werden:
Die XML-Datei für die Z-Posen wird für ein C-Programm benötigt. Dies ist eine Vorbereitung für den nächsten Schritt.
(Weitere Informationen über XML unter http://www.xmlfox.com/index.htm)
In der Tabelle 9 wird ein Teil von XML-Datei für die Folgeposen-Tabelle ("Bow") gezeigt, die Elemente- und Attribute-Namen in XML-Dateien haben foldende Bedeutungen:
- NewDataSet: das einzig zulässige Wurzelement
- PARTS: die Kindelemente von <NewDataSet>
- insertBewegung: der Name der eingefügte Grundbewegung
- PART: einige Kindelemente von <PARTS>
- Bewegungsnamen: der Name der Grundewegungen
- BewegungsFolge: eine Z-Pose zu einem bestimmte Zeitpunkt
- Naechst_Folge: ein Nachfolger einer Z-Pose in der Grundbewegung
- Mehre_Folgeposen: alle Folgeposen einer Z-Pose
- Haupt_Folgeposen: die bestene Folgeposen aus aller Folgeposen
In Tabelle 9 wird ein Teil von XML-Folgeposen-Tabelle "Bow" gezeigt. Diese XML-Datei ist eine Vorbereitung der Arbeit für die anderen Gruppe.
  <?xml version="1.0" standalone="yes" ?> <NewDataSet> <Parts> <insertBewegung>1_Bow</insertBewegung> <PART> <Bewegungsname>2_Hands up</Bewegungsname> <Bewegungsfolge>HU_p1</Bewegungsfolge> <Naechst_Folge>HU_sp</Naechst_Folge> <Mehre_Folgeposen>B_z1, B_z2</Mehre_Folgeposen> <Haupt_Folgeposen>B_z1</Haupt_Folgeposen> </PART> <PART> <Bewegungsfolge>HU_sp</Bewegungsfolge> <Naechst_Folge>HU_p1</Naechst_Folge> <Mehre_Folgeposen>B_z1, B_z2</Mehre_Folgeposen> <Haupt_Folgeposen>B_z1</Haupt_Folgeposen>  </PART>           ...     </Parts>
... Â Â Â </NewDataSet> |
               Tabelle 9:ein Teil von XML-Datei für die Folgeposen-Tabelle
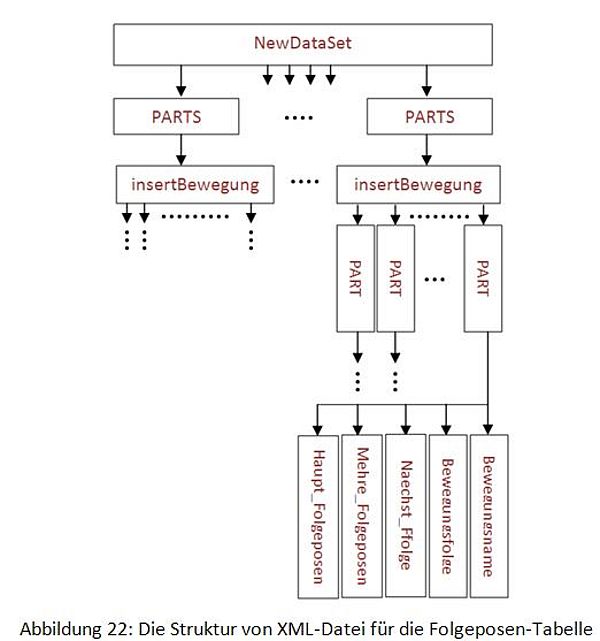
Die Abbildung 22 zeigt die Struktur der XML-Datei für die Nachfolgerelation.
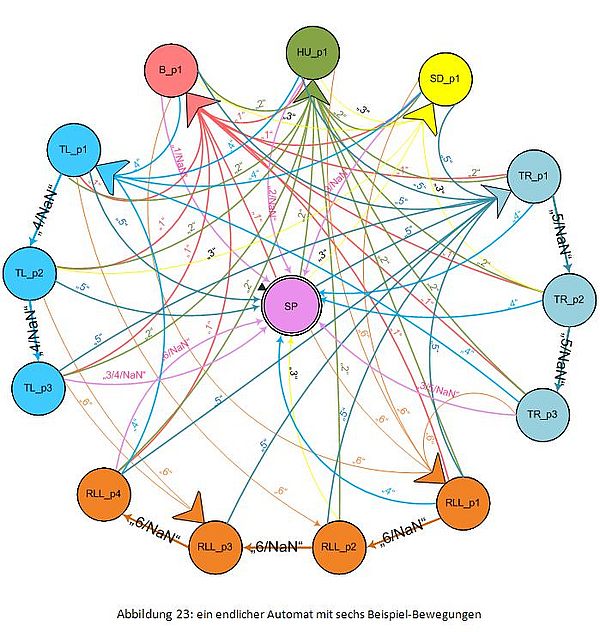
Diese vollständige Nachfolgerelationen werden auch durch einen endlichen Automat beschrieben. Aber dieser Automat ist sehr kompliziert und damit unlesbar. In der Abbildung23 wird ein endlicher Automat mit sechs Beispiel-Bewegungen ("Bow", "Hands_up", "Sit_down", "Turn_left", "Turn_right" und auch "Raise_left_leg") gezeigt.
Programm 1
a. Sinn und Zweck des Programms
Bei der originalen Programmstruktur muss eine Bewegung vollständig ablaufen, damit die nachfolgende Bewegung weiter ablaufen kann. D.h., wenn der Roboter auf ein Problem (z.B. ein Hindernissen) trifft, kann er keine richtige Behandlung ausführen. Bei dem Programm 1 können die Grundbewegungen nach jeder Z-Pose abgebrochen werden, um neue Bewegungen auszuführen.
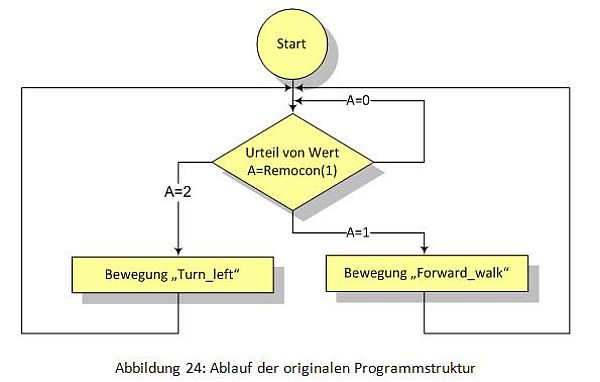
In der Abbildung 24 wird die originale Struktur mit zwei Beispiel-Bewegungen ("Forward_walk" und "Turn_left") gezeigt.
b. Algorithmus
Hieraus entsteht eine neue Programmstruktur: Nach jeder Z-Pose fragt der Roboter nach, ob eine Taste gedrückt wird; wenn ja, wird die Bewegung von der gerade getanen Pose zu ihrer passenden Haupt-Folgepose gesprungen; sonst wird die Bewegung nur weiter durchgeführt.
c. Realisierung des Programms
I. Realisierung 1
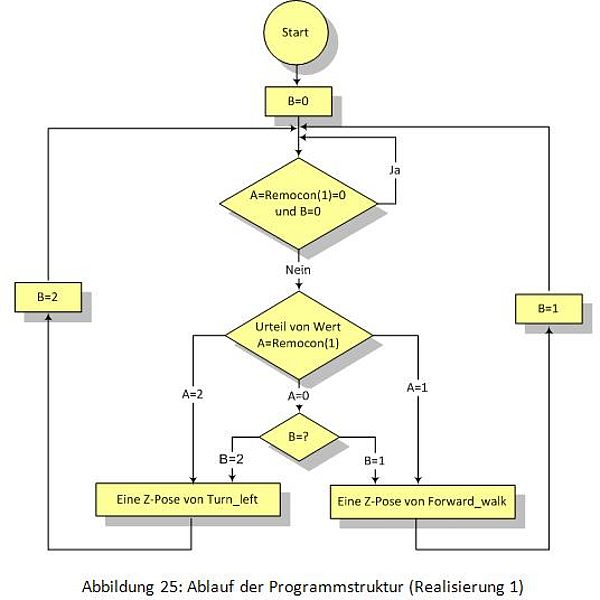
- In der Abbildung 25 wird die Struktur für Realisierung 1 mit zwei Beispiel-Bewegungen ("Forward_walk" und "Turn_left") gezeigt.
Der Roboter fragt nach jeder Z-Pose nach, ob eine Taste gedrückt wird. Falls der Befehl "REMOCON" benutzt wird, dauert diese Nachfrage eine relativ lange Zeit. Deshalb bewegt sich der Roboter nicht mehr flüssig.
II. Realisierung 2
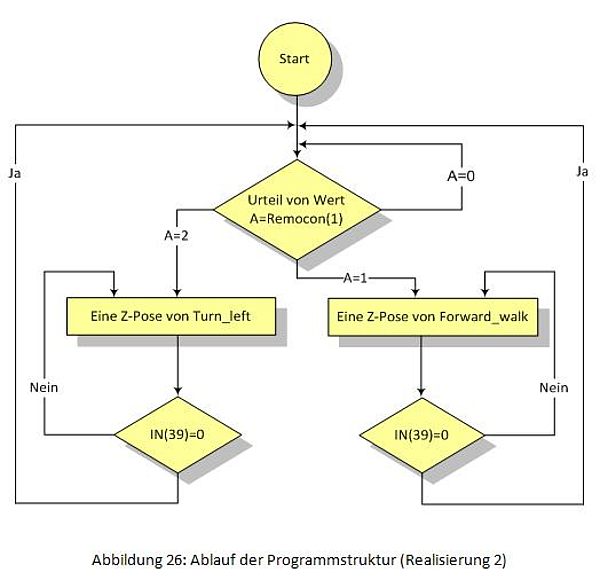
Um das Problem, das es bei Realisierung 1 gibt, zu lösen, wird der Befehl "IN(39)" aus 'input port' benutzt, weil er nur eine kurze Zeit benötigt. Das bedeutet, nur wenn eine Taste gedrückt wird, dann fragt das Programm sie nach; sonst fragt es nicht nach und wird nur weiter ausführt. Damit bewegt sich der Roboter flüssiger als früher. In der Abbildung 26 wird diese verbesserte Struktur gezeigt.
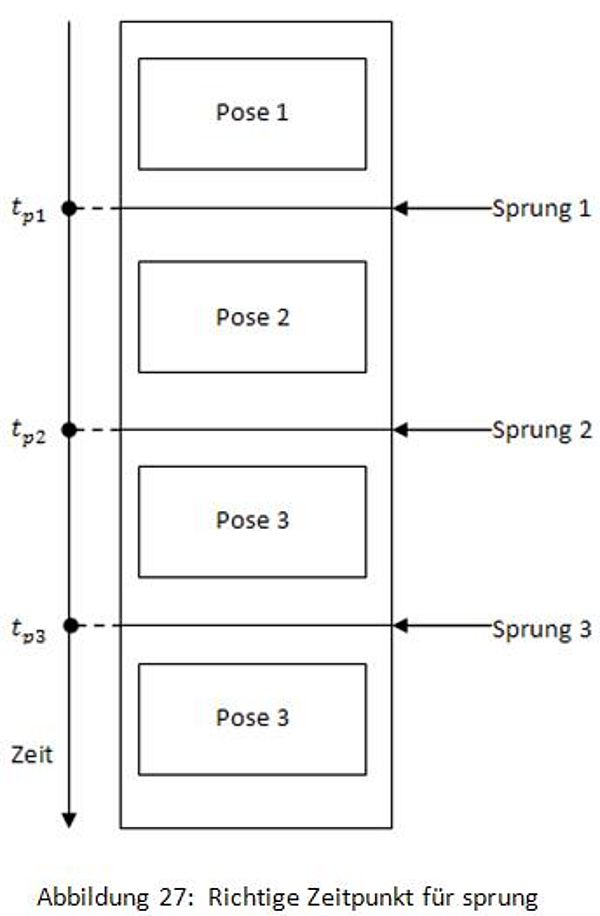
Es kann jedoch auftreten, dass eine neue Taste gedrückt wird, ohne dass der Roboter reagiert. D.h., diese Taste ist nicht aktiviert worden, weil sie zu einem bestimmten Zeitpunkt (tp) gedrückt werden muss. (Abbildung 27)
Unten werden die Verknüpfungen der Flussdiagramme vom Befehl "IN(n)" und "REMOCON(1)" erklärt.
REMOCON (1):
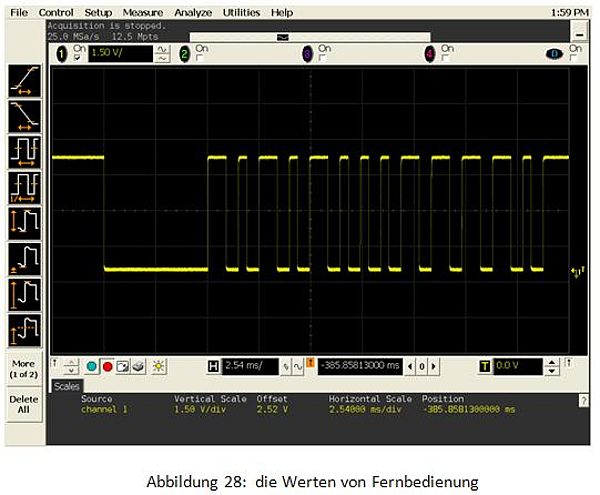
Nach jeder Z-Pose fragt das Programm nach, ob eine Taste gedrückt wird. Wenn ja, wird von der geeigneten Z-Pose zu ihrer Haupt-Folgepose gesprungen; sonst wird die Bewegung weiter durchgeführt. Um immer nachfragen zu können, wird der Befehl "REMOCON" immer ausgeführt. Aber "REMOCON" muss alle Werte der Infrarot-Bedienung einlesen, d.h. es dauert relativ lange, womit die Bewegung nicht mehr flüssig ist. Das Signal der Infrarot-Bedienung dauert 20ms an, wie die folgende Abbildung 28 zeigt:
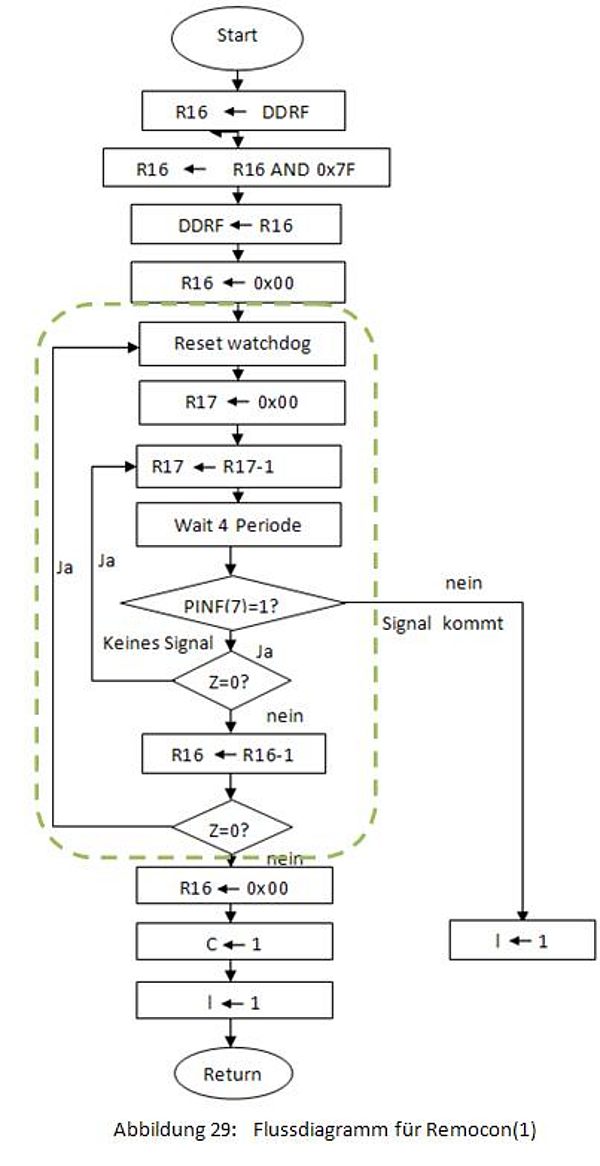
Wird die Taste nicht gedrückt, wird der Befehl "REMOCON" dennoch ausgeführt. Das Flussdiagramm für "REMOCON" wird in der Abbildung 29 gezeigt. Der mit der gestrichelten Linie ausgewählte Teil hat zwei Schleifen. Die erste Schleife ist von "Reset Wachtdog" bis zum zweiten "Z=0?". Die zweite Schleife ist von "R17 ← R17-1" bis zum ersten "Z=0?". Wenn der Befehl "REMOCON" durchgeführt wird, müssen die zwei Schleifen durchlaufen werden. Jede Schleife zählt dabei 256 Mal, d.h., die "REMOCON" wird 65536 (256*256) mal zählen. Das ist ein großer Zeitaufwand. Diese Eigenschaft von "REMOCON" führt dazu, dass die Bewegung nicht flüssig ist.
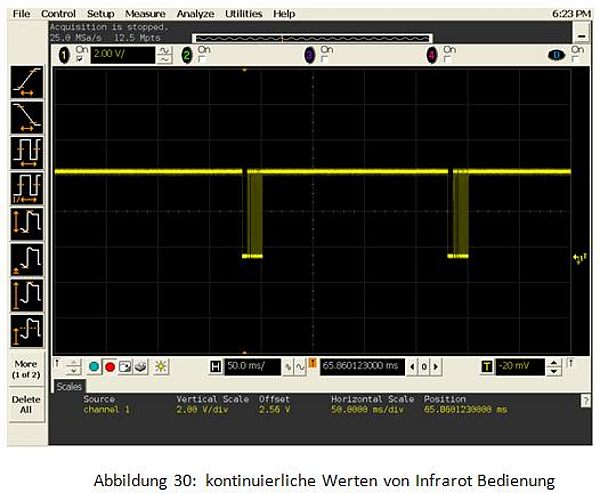
Um diesen Zeitaufwand zu verkürzen, wird ein neuer Befehl benutzt. Dies ist "In(39)" (oder "AD(7)"). "In(39)" liest nur den ersten Hochpegel aller Werte von der Infrarot Bedienung (Abbildung 30). Wenn der Pegel immer "Hoch" bleibt, das heißt, dass kein Signal kommt, wird "REMOCON" nicht abgefragt. Wenn der Pegel sich verändert, das heißt, dass das neue Signal kommt, dann liest "REMOCON" das Signal.
Unten sind die Verweise auf die Flussdiagramme von IN(n) und REMOCON(1) angegeben, die von anderen Gruppen erstellt worden sind.
Dateien
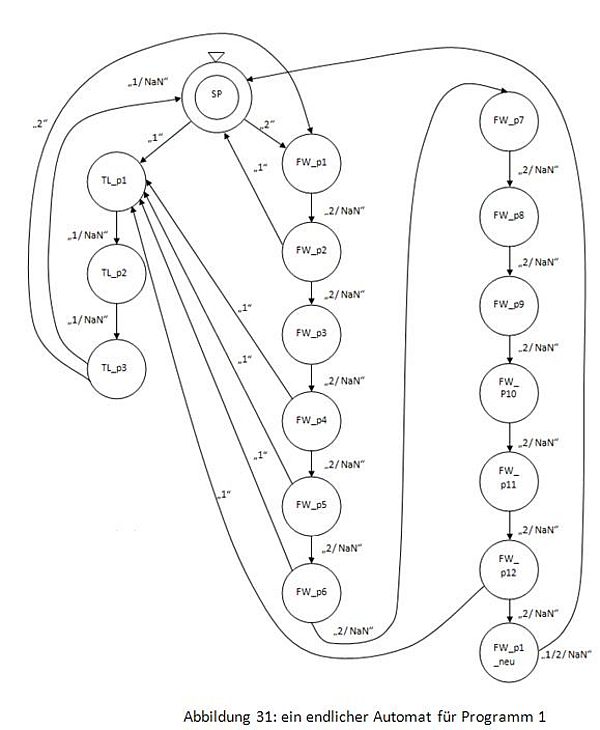
Die Realisierung 1 und 2 kann man auch unter einem endlichen Automat (Abbildung 31) verstehen.
d. Erweiterung des Programms
Bei dem Algorithmus von Programm 1 muss eine neue Taste im richtigen Moment gedrückt werden. Sonst wird sie nicht aktiviert.
- Interrupt:
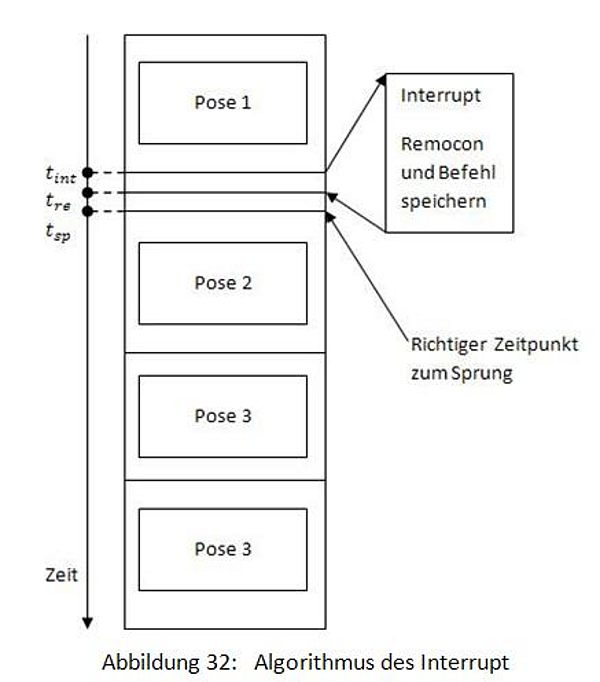
Den folgenden Algorithmus kann in weiteren Projekten verwendet werden. Außerdem funktioniert er besser, wenn das Unterprogramm (REMOCON) mit Interrupt verbunden wird, wobei REMOCON als parallel laufendes Programm bezeichnet wird. D.h., der neue Befehl (gedrückte Taste) kann immer eingelesen und auch in einem Buffer behalten werden, bis das Hauptprogramm nach einer Z-Pose zu einer passenden Z-Pose springen kann. Diese Idee wird in Abbildung 32 gezeigt.
e. Das Quellcode
Programm 2
a. Sinn und Zweck des Programms
Um die Bewegung-Bibliotheken zu testen, wird "Programm 2" geschrieben. Wegen der Einschränkung des RoboBASIC wird eine höhere Programmiersprache (C-Sprache) verwendet. Dieses geschriebene "Programm 2" kann flexibel bearbeitet und weiter angewendet werden.
b. Algorithmus
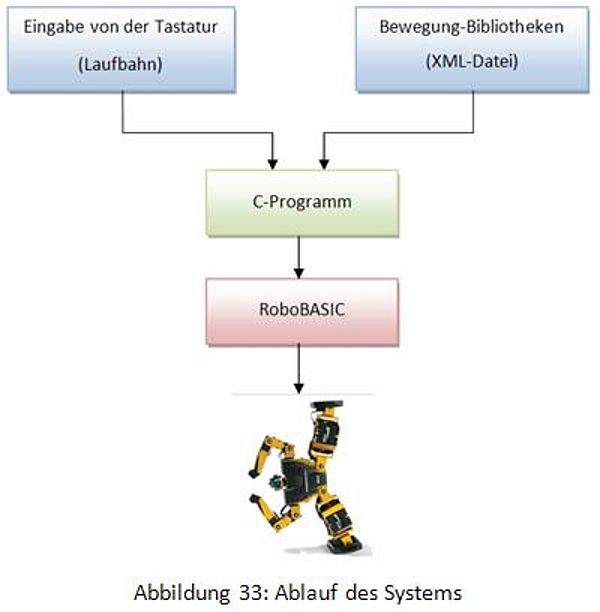
- In der Quell-Datei für den Compiler befindet sich eine Reihe von Punkten (Ablaufbahn). Durch diese vom Benutzer definierte Bahn muss der Roboter gehen.
- Die Bibliothek ist Die XML-Datei.
- Die Ziel-Datei wird das RoboBASIC-Programm sein, das später im Mikrokontroller Atmega128 zu finden ist.
Der Ablauf durch die Bahn ist durch drei unterschiedliche Möglichkeiten zu realisieren.
c. Realisierung des Programms
I. Realisierung 1
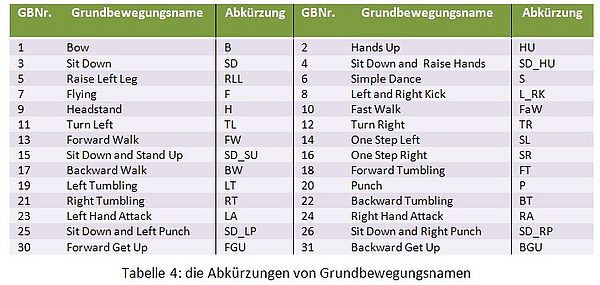
- Bei dieser Methode werden vier Bewegungen benutzt. Sie sind "One_step_left", "One_step_right", "Forward_walk" und "Backward_walk".
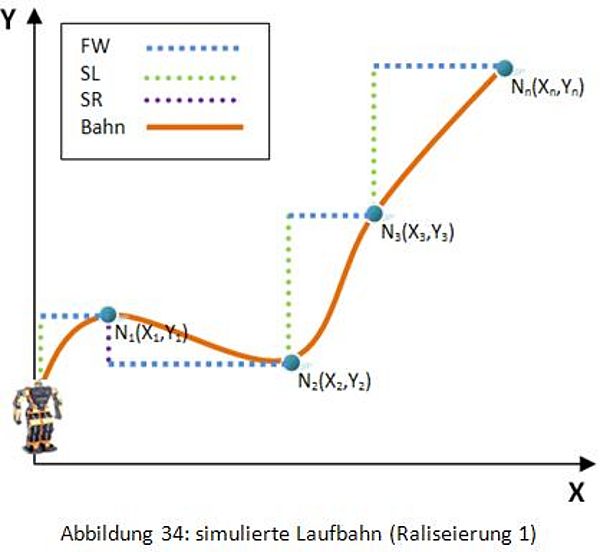
Zuerst werden die Koordinaten von einigen Punkten eingegeben. Dann wird berechnet, wie viele Schritte sich der Roboter nach links oder rechts bewegen soll und wie viele Schritte er geradeaus oder rückwärts gehen soll. Gleichzeitig werden die geeigneten Grundbewegungen aus der XML-Datei ausgewählt. Schließlich wird der ganze Prozess in eine TXT-Datei geschrieben. In dieser Realisierung (Abbildung 34) bewegt sich der Roboter in einem Zug oder zwei Zügen zwischen zwei Punkten.
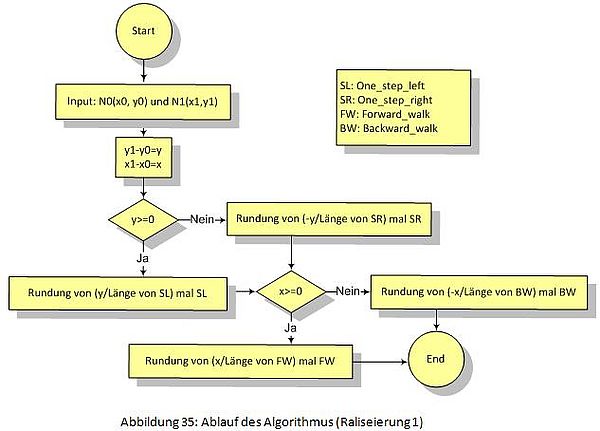
Algorithmus:
In dieser Realisierung lässt sich die Richtung, in die der Roboter steht, am Anfang als positive Richtung der X-Achse definieren. Dann befindet sich links vom Roboter die positive Richtung der Y-Achse.
- Zwischen jeden zwei Punkten (z.B. N0(X0,Y0) und N1(X1,Y1)) werden X = X1 - X0 und Y = Y1-Y0 berechnet. (N0 ist der Punkt,auf dem der Roboter steht. N1 ist der Punkt,zu dem der Roboter geht.)
- Dann lässt sich entscheiden: wenn X > 0, geht der Roboter nach vorne (FW, Kurzname von "Forward_walk"), wenn X < 0, nach hinten (BW, Kurzname von "Backward_walk"); wenn Y > 0, geht der Roboter ein Schritt nach links (SL, Kurzname von "One_step_left"), wenn X < 0, nach rechts (SR, Kurzname von "One_step_right").
- |X|/(Länge des FW) oder |X|/(Länge des BW) bedeutet, wie viele Schritte der Roboter nach vorne oder nach hinten gehen soll. Hier lässt sich das Ergebnis abrunden, weil der Roboter keinen halben Schritt machen kann. Ebenso bedeutet |Y|/(Länge des SL) oder |Y|/(Länge des SR), wie viele Schritte der Roboter nach links oder nach rechts gehen soll. Hier lässt sich das Ergebnis auch abrunden.
II. Realisierung 2
Bei dieser Methode werden drei Bewegungen benutzt. Diese sind "Turn_left", "Turn_right" und "Forward_walk".
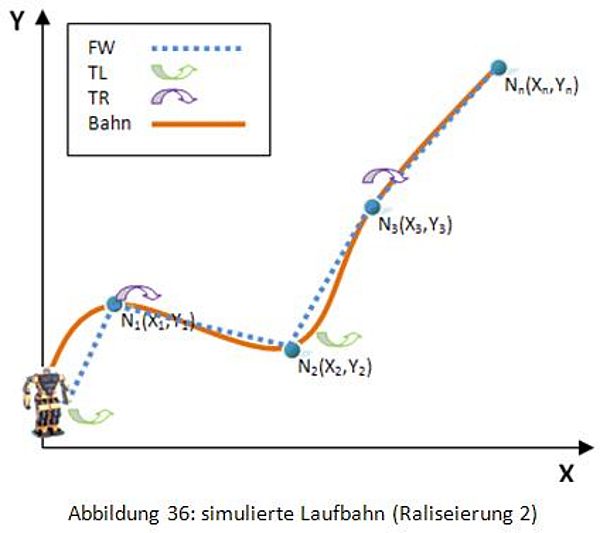
Zuerst werden ebenfalls die Koordinaten von drei Punkten eingegeben. Dann wird berechnet, um wie viel Grad sich der Roboter drehen soll und wie viele Schritte er gehen soll. Gleichzeitig werden die geeigneten Bewegungen aus der XML-Datei extrahiert. Anschließend wird der ganze Prozess in eine TXT-Datei geschrieben. In diesem Schritt (Abbildung 36) bewegt sich der Roboter nur in einem Zug zwischen zwei Punkten.
Algorithmus:
In dieser Realisierung lässt sich die Richtung, in die der Roboter steht, am Anfang auch als positive Richtung der X-Achse definieren. Dann befindet sich links vom Roboter die positive Richtung der Y-Achse.
- Zuerst werden k1 = 0 (am Anfang), k2 = atan2(Y2-Y1, X2-X1) [hier sind k1 und k2 zwischen -&pi und &pi ] und d (Abstand zwischen N1 und N2) zwischen zwei Punkten (N1(X1,Y1) und N2(X2,Y2)) berechnet. (N1 ist der Punkt,auf dem der Roboter steht. N2 ist der Punkt,zu dem der Roboter geht.)
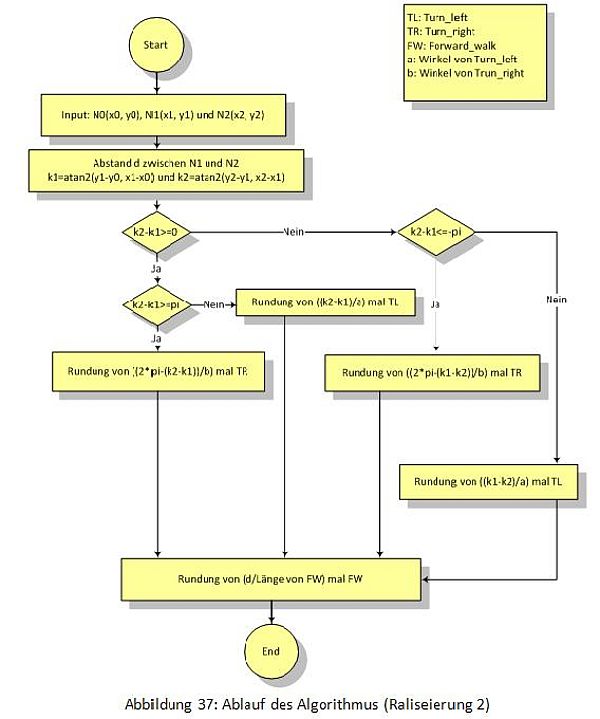
- Dann lässt sich entscheiden:
- Wenn k2 - k1 ≥ &pi, dann dreht sich der Roboter {(2*&pi - (k2 - k1))/b} mal nach rechts; [hier b: Drehwinkel von einmal "Turn_right"]
- Wenn 0 ≤ k2 - k1 < &pi, dann dreht sich der Roboter {(k2 - k1)/a} mal nach links; [hier a: Drehwinkel von einma] "Turn_left"]
- Wenn k2 - k1 ≤ -&pi, dann dreht sich der Roboter {(2*&pi - (k1 - k2))/b} mal nach rechts;
- Wenn -&pi < k2 - k1 < 0, dann dreht sich der Roboter {(k1 - k2)/a} mal nach links;
- |d|/(Länge der FW) bedeutet, wie viel Schritte der Roboter nach vorne gehen soll.
- Danach werden werden k1 = atan2(Y1-Y0, X1-X0), k2 = atan2(Y2-Y1, X2-X1) und d (Abstand zwischen N1 und N2) zwischen zwei Punkten (N1(X1, Y1) und N2(X2, Y2)) berechnet. (N1 ist der Punkt, auf dem der Roboter jetzt steht. N2 ist der Punkt, zu dem der Roboter geht. N0 ist der Punkt, auf dem der Roboter im letzten Status stand.)
- Dann wird b) und c) wiederholt. Gemäß dieser Methode wird die Laufbahn des Roboters berechnet.
- Hier lassen sich alle Ergebnisse abrunden, weil der Roboter keinen halben Schritt gehen oder keine halbe Drehung durchführen kann.
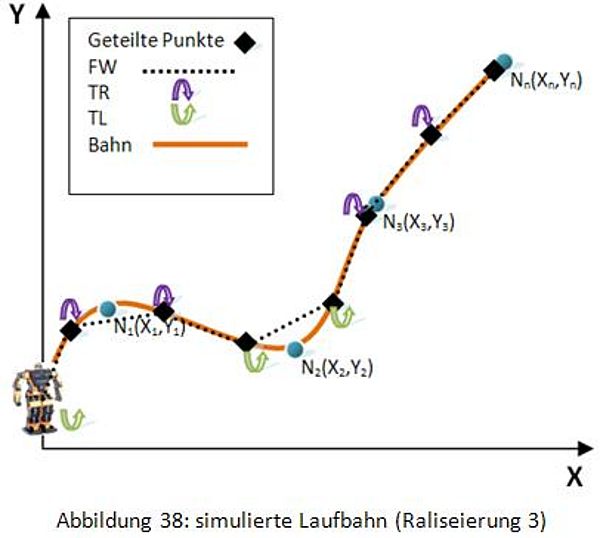
III. Realisierung 3
Zuerst wird eine glatte Kurve vom Startpunkt bis zum Endpunkt erzeugt. Anschließend wird die Länge der Kurve berechnet. Gemäß der Länge wird die Kurve in viele gleiche kleine Abschnitte geteilt. Dann werden die Koordinaten der geteilten Punkte berechnet. Der Roboter wird durch diese Koordinatenpunkte gehen. Die restlichen Schritte sind wie in Methode 2.
Diese Methode ist nur ein Entwurf. Ihr entsprechendes Programm ist in dieser Arbeit nicht realisiert worden.
IV. Grunddaten
Im Folgenden werden die Daten von einem Drehwinkel, der Länge einer Schrittweite nach vorne, nach links, nach rechts, und nach hinten des Roboters gezeigt. Gemäß dieser Daten kann einfach berechnet werden, wie oft der Roboter sich drehen oder gehen soll.
Eine Schrittweite von "Forward_walk" beträgt ca. 4,7 cm, eine Schrittweite von "Backward_Walk" ca. 4,3 cm. Die Länge eines Schrittes von "One_Step_left" und "One_Step_Right" misst ca. 10cm und 10cm. Die Größe des Drehwinkels (Links und Rechts) ist ca. 15 Grad.
Wegen der Eigenschaften des Metalls und der Nullpunktseinstellung ist die Größe der Schrittweite und Drehwinkels (Links und Rechts) nicht fest.
Fazit
In dieser Arbeit wird die Bewegungsbibliothek entwickelt. Diese Bibliothek ist die Basis für weitere Forschungen der Bewegung.
Die Bewegungsbibliothek besteht aus zwei WORD-Dateien und zwei entsprechenden XML-Dateien. In den WORD-Dateien können die Posen und die Z-Posen und auch ihre Nachfolgerelation anschaulich verstanden werden. Die XML-Dateien können in vielen Programmiersprachen verwendet werden.
Um diese Bewegungsbibliothek zu testen, werden zwei unterschiede Programmiersprachen eingesetzt.
Eine ist die RoboBASIC-Sprache. In diesem RoboBASIC-Programm kann die gerade ausgeführte Bewegung des Roboters abgebrochen werden. Mit Hilfe einer schon aufgestellten Nachfolgerelation kann der Roboter durch die Fernbedingung eine weitere Bewegung sofort ausführen.
Die andere Programmiersprache ist C-Sprache. Im C-Programm wird ein RoboBASIC-Programm gemäß der gewünschten Laufbahn automatisch in eine TXT-Datei umgewandelt. Der Roboter kann sich dabei drei unterschiedlicher Methoden bedienen, um sich über die Laufbahn zu bewegen. Die dritte Methode ist am besten, aber sie ist nur ein theoretischer Entwurf. Wegen der Komplexität des Algorithmus kann diese Methode nur schwer realisiert werden. In der Praxis ist die zweite Methode besser als die Erste, da keine Zwischenschritte gemacht werden müssen.
Achtung:
1) Die RoboBASIC-Sprache hat auch einige Einschränkungen. So können beispielsweise viele Befehle der Sprache nicht durchgeführt werden, z.B. :
- Mehrere if-Bedienungen können nicht untereinander geschrieben werden,
- if A then
- if B then
Es muss richtig heißen:
- If A and B then
- if A then
- Das Kompilieren mehrerer Bedingungen (mit "and" oder "or") miteinander im if-Befehl ist nicht möglich. Es können nur maximal zwei Bedingungen verwendet werden.
- if A and B and C then
Der Befehl muss folgendermaßen geschrieben werden:
- if A and neu_Var then (neu_Var=[ein Werte abzüglich zum B und C])
Bei einer weiteren Bearbeitung sollten die Befehle des RoboBASIC berücksichtigt werden. Bei mehreren if-Bedingungen ist jedoch ein hoher Zeitaufwand nötig, der mit dem Befehl "GOSUB" vermieden werden kann. Zusätzlich würde sich eine weitere Untersuchung und Betrachtung der Kombination der Bewegung anbieten.
2) Im C-Programm existiert ein Algorithmus für die Näherung.
Die Schrittweite des Roboters ist bereits festgelegt. Wenn der gegebene Abstand nicht durch diese Schrittweite teilbar ist, dann wird das Ergebnis abgerundet. Beim Drehwinkel gibt es die gleiche Näherung. D.h. der Roboter braucht noch einen Orientierungssensor.